Computer Logical Organization - Overview
In the modern world of electronics, the term Digital is generally associated with a computer because the term Digital is derived from the way computers perform operation, by counting digits. For many years, the application of digital electronics was only in the computer system. But now-a-days, digital electronics is used in many other applications. Following are some of the examples in which Digital electronics is heavily used.
Industrial process controlMilitary systemTelevisionCommunication systemMedical equipmentRadarNavigation
Signal
Signal can be defined as a physical quantity, which contains some information. It is a function of one or more than one independent variables. Signals are of two types.
Analog SignalDigital Signal
Analog Signal
An analog signal is defined as the signal having continuous values. Analog signal can have infinite number of different values. In real world scenario, most of the things observed in nature are analog. Examples of the analog signals are following.
TemperaturePressureDistanceSoundVoltageCurrentPower
Graphical representation of Analog Signal (Temperature)
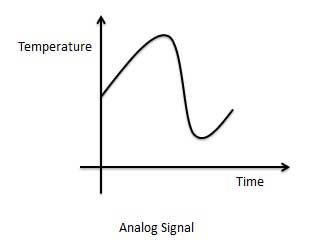
The circuits that process the analog signals are called as analog circuits or system. Examples of the analog system are following.
FilterAmplifiersTelevision receiverMotor speed controller
Disadvantage of Analog Systems
Less accuracyLess versatilityMore noise effectMore distortionMore effect of weather
Digital Signal
A digital signal is defined as the signal which has only a finite number of distinct values. Digital signals are not continuous signals. In the digital electronic calculator, the input is given with the help of switches. This input is converted into electrical signal which have two discrete values or levels. One of these may be called low level and another is called high level. The signal will always be one of the two levels. This type of signal is called digital signal. Examples of the digital signal are following.
Binary SignalOctal SignalHexadecimal Signal
Graphical representation of the Digital Signal (Binary)
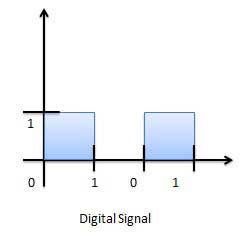
The circuits that process the digital signals are called digital systems or digital circuits. Examples of the digital systems are following.
RegistersFlip-flopCountersMicroprocessors
Advantage of Digital Systems
More accuracyMore versatilityLess distortionEasy communicatePossible storage of information
Comparison of Analog and Digital Signal
S.N.Analog SignalDigital Signal1Analog signal has infinite values.Digital signal has a finite number of values.2Analog signal has a continuous nature.Digital signal has a discrete nature.3Analog signal is generated by transducers and signal generators.Digital signal is generated by A to D converter.4Example of analog signal − sine wave, triangular waves.Example of digital signal − binary signal.
Digital Number System
A digital system can understand positional number system only where there are a few symbols called digits and these symbols represent different values depending on the position they occupy in the number.
A value of each digit in a number can be determined using
The digit
The position of the digit in the number
The base of the number system (where base is defined as the total number of digits available in the number system).
Decimal Number System
The number system that we use in our day-to-day life is the decimal number system. Decimal number system has base 10 as it uses 10 digits from 0 to 9. In decimal number system, the successive positions to the left of the decimal point represents units, tens, hundreds, thousands and so on.
Each position represents a specific power of the base (10). For example, the decimal number 1234 consists of the digit 4 in the units position, 3 in the tens position, 2 in the hundreds position, and 1 in the thousands position, and its value can be written as
(1×1000) + (2×100) + (3×10) + (4×l) (1×103) + (2×102) + (3×101) + (4×l00) 1000 + 200 + 30 + 1 1234
As a computer programmer or an IT professional, you should understand the following number systems which are frequently used in computers.
S.N.Number System & Description1Binary Number System
Base 2. Digits used: 0, 1
2Octal Number System
Base 8. Digits used: 0 to 7
3Hexa Decimal Number System
Base 16. Digits used: 0 to 9, Letters used: A- F
Binary Number System
Characteristics
Uses two digits, 0 and 1.
Also called base 2 number system
Each position in a binary number represents a 0 power of the base (2). Example: 20
Last position in a binary number represents an x power of the base (2). Example: 2x where x represents the last position - 1.
Example
Binary Number: 101012
Calculating Decimal Equivalent −
StepBinary NumberDecimal NumberStep 1101012((1 × 24) + (0 × 23) + (1 × 22) + (0 × 21) + (1 × 20))10Step 2101012(16 + 0 + 4 + 0 + 1)10Step 31010122110
Note: 101012 is normally written as 10101.
Octal Number System
Characteristics
Uses eight digits, 0,1,2,3,4,5,6,7.
Also called base 8 number system
Each position in an octal number represents a 0 power of the base (8). Example: 80
Last position in an octal number represents an x power of the base (8). Example: 8x where x represents the last position - 1.
Example
Octal Number − 125708
Calculating Decimal Equivalent −
StepOctal NumberDecimal NumberStep 1125708((1 × 84) + (2 × 83) + (5 × 82) + (7 × 81) + (0 × 80))10Step 2125708(4096 + 1024 + 320 + 56 + 0)10Step 3125708549610
Note: 125708 is normally written as 12570.
Hexadecimal Number System
Characteristics
Uses 10 digits and 6 letters, 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F.
Letters represents numbers starting from 10. A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.
Also called base 16 number system.
Each position in a hexadecimal number represents a 0 power of the base (16). Example 160.
Last position in a hexadecimal number represents an x power of the base (16). Example 16x where x represents the last position - 1.
Example −
Hexadecimal Number: 19FDE16
Calculating Decimal Equivalent −
StepBinary NumberDecimal NumberStep 119FDE16((1 × 164) + (9 × 163) + (F × 162) + (D × 161) + (E × 160))10Step 219FDE16((1 × 164) + (9 × 163) + (15 × 162) + (13 × 161) + (14 × 160))10Step 319FDE16(65536 + 36864 + 3840 + 208 + 14)10Step 419FDE1610646210
Note − 19FDE16 is normally written as 19FDE.
Number System Conversion
There are many methods or techniques which can be used to convert numbers from one base to another. We'll demonstrate here the following −
Decimal to Other Base SystemOther Base System to DecimalOther Base System to Non-DecimalShortcut method − Binary to OctalShortcut method − Octal to BinaryShortcut method − Binary to HexadecimalShortcut method − Hexadecimal to Binary
Decimal to Other Base System
Steps
Step 1 − Divide the decimal number to be converted by the value of the new base.
Step 2 − Get the remainder from Step 1 as the rightmost digit (least significant digit) of new base number.
Step 3 − Divide the quotient of the previous divide by the new base.
Step 4 − Record the remainder from Step 3 as the next digit (to the left) of the new base number.
Repeat Steps 3 and 4, getting remainders from right to left, until the quotient becomes zero in Step 3.
The last remainder thus obtained will be the Most Significant Digit (MSD) of the new base number.
Example −
Decimal Number: 2910
Calculating Binary Equivalent −
StepOperationResultRemainderStep 129 / 2141Step 214 / 270Step 37 / 231Step 43 / 211Step 51 / 201
As mentioned in Steps 2 and 4, the remainders have to be arranged in the reverse order so that the first remainder becomes the Least Significant Digit (LSD) and the last remainder becomes the Most Significant Digit (MSD).
Decimal Number − 2910 = Binary Number − 111012.
Other Base System to Decimal System
Steps
Step 1 − Determine the column (positional) value of each digit (this depends on the position of the digit and the base of the number system).
No comments:
Post a Comment